Xem tài liệu

>>Cho hàm số y =f(x). Tìm số nghiệm thực phân biệt của phương trình g(f(x))=0

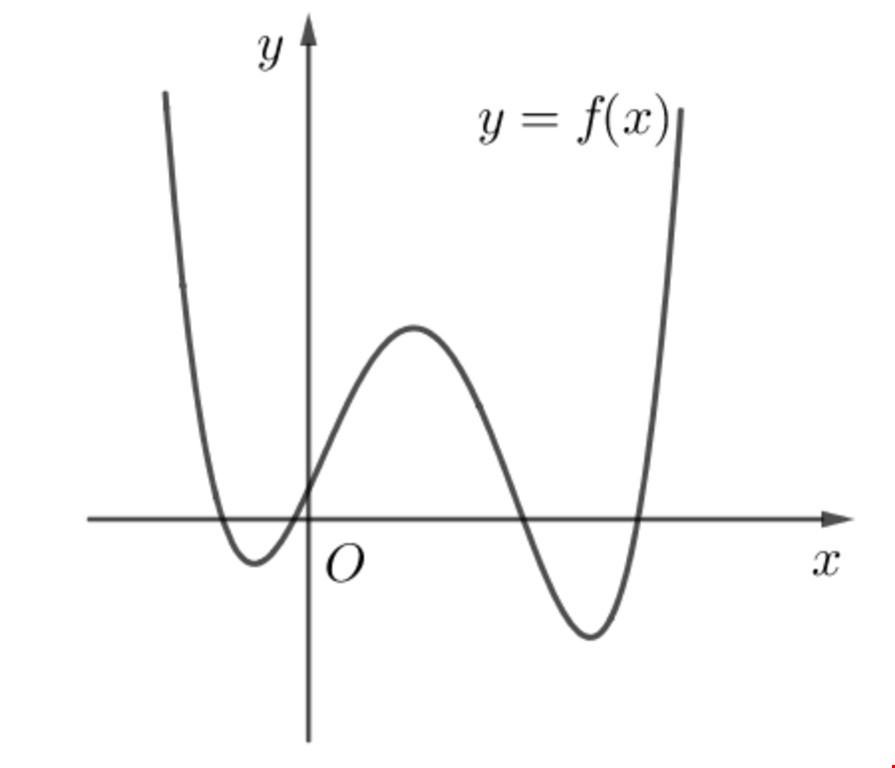
Cho $f(x)$ là một hàm đa thức bậc bốn có đồ thị như hình vẽ bên. Tập nghiệm của phương trình ${{({f}'(x))}^{2}}=f(x).{f}''(x)$ có số phần tử là

A. $6.$

B. $2.$

C. $4.$

D. $0.$

Lời giải chi tiết: Đồ thị hàm $f(x)$ cắt trục hoành tại bốn điểm phân biệt và $f(x)$ là hàm đa thức bậc bốn nên $f(x)=a(x-{{x}_{1}})(x-{{x}_{2}})(x-{{x}_{3}})(x-{{x}_{4}})$ với ${{x}_{1}}<{{x}_{2}}<{{x}_{3}}<{{x}_{4}}$ và $a>0.$

Thực hiện lấy đạo hàm ta có:${f}'(x)=f(x)left( frac{1}{x-{{x}_{1}}}+frac{1}{x-{{x}_{2}}}+frac{1}{x-{{x}_{3}}}+frac{1}{x-{{x}_{4}}} right),forall xin mathbb{R}backslash left{ {{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}} right}.$

Suy ra $frac{{f}'(x)}{f(x)}=frac{1}{x-{{x}_{1}}}+frac{1}{x-{{x}_{2}}}+frac{1}{x-{{x}_{3}}}+frac{1}{x-{{x}_{4}}}.$

Tiếp tục lấy đạo hàm hai vế ta có:

$frac{{f}''(x).f(x)-{{({f}'(x))}^{2}}}{{{(f(x))}^{2}}}=-frac{1}{{{(x-{{x}_{1}})}^{2}}}-frac{1}{{{(x-{{x}_{2}})}^{2}}}-frac{1}{{{(x-{{x}_{3}})}^{2}}}-frac{1}{{{(x-{{x}_{4}})}^{2}}}<0,forall xin mathbb{R}backslash left{ {{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}} right}.$

Vậy ${f}''(x).f(x)-{{({f}'(x))}^{2}}<0,forall xin mathbb{R}backslash left{ {{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}} right}.$

Tại các điểm ${{x}_{i}},i=1,2,3,4$ thì ${f}''({{x}_{i}}).f({{x}_{i}})=0<{{({f}'({{x}_{i}}))}^{2}}.$

Vậy ${f}''(x).f(x)-{{({f}'(x))}^{2}}<0,forall xin mathbb{R},$ tức phương trình đã cho vô nghiệm. Chọn đáp án D.

*Mẹo trắc nghiệm: Vì đề bài cho đúng với mọi hàm đa thức bậc bốn có 4 nghiệm phân biệt nên ta chỉ cần chọn một hàm số đa thức bậc bốn có bốn nghiệm phân biệt, chẳng hạn: $f(x)=({{x}^{2}}-1)({{x}^{2}}-2)={{x}^{4}}-3{{x}^{2}}+2.$ Khi đó ${f}'(x)=4{{x}^{3}}-6x;{f}''(x)=12{{x}^{2}}-6.$

Xét phương trình ${{(4{{x}^{3}}-6x)}^{2}}=({{x}^{4}}-3{{x}^{2}}+2)(12{{x}^{2}}-6)Leftrightarrow 2{{x}^{6}}-3{{x}^{4}}-3{{x}^{2}}+6=0$ phương trình vô nghiệm. Chọn đáp án D.

>>Bài tập dành cho bạn đọc tự luyện:

Gồm 4 khoá luyện thi duy nhất và đầy đủ nhất phù hợp với nhu cầu và năng lực của từng đối tượng thí sinh:

Bốn khoá học X trong gói COMBO X 2019 có nội dung hoàn toàn khác nhau và có mục đich bổ trợ cho nhau giúp thí sinh tối đa hoá điểm số.

1. PRO X 2019: Luyện thi THPT Quốc Gia 2019 - Học toàn bộ chương trình Toán 12, luyện nâng cao Toán 10 Toán 11 và Toán 12. Khoá này phù hợp với tất cả các em học sinh vừa bắt đầu lên lớp 12 hoặc lớp 11 học sớm chương trình 12, Học sinh các khoá trước thi lại đều có thể theo học khoá này. Mục tiêu của khoá học giúp các em tự tin đạt kết quả từ 8 đến 9 điểm.
2. PRO XMAX 2019: Luyện nâng cao 9 đến 10 chỉ dành cho học sinh giỏi Học qua bài giảng và làm đề thi nhóm câu hỏi Vận dụng cao trong đề thi THPT Quốc Gia thuộc tất cả chủ đề đã có trong khoá PRO X. Khoá PRO XMAX học hiệu quả nhất khi các em đã hoàn thành chương trình kì I Toán 12 (tức đã hoàn thành Logarit và Thể tích khối đa diện) có trong Khoá PRO X. Mục tiêu của khoá học giúp các em tự tin đạt kết quả từ 8,5 đếm 10 điểm.
3. PRO XPLUS 2019: Luyện đề thi tham khảo THPT Quốc Gia 2019 Môn Toán gồm 20 đề 2019. Khoá này các em học đạt hiệu quả tốt nhất khoảng thời gian sau tết âm lịch và cơ bản hoàn thành chương trình Toán 12 và Toán 11 trong khoá PRO X. Khoá XPLUS tại Vted đã được khẳng định qua các năm gần đây khi đề thi được đông đảo giáo viên và học sinh cả nước đánh giá ra rất sát so với đề thi chính thức của BGD. Khi học tại Vted nếu không tham gia XPLUS thì quả thực đáng tiếc.
4. PRO XMIN 2019: Luyện đề thi tham khảo THPT Quốc Gia 2019 Môn Toán từ các trường THPT Chuyên và Sở giáo dục đào tạo, gồm các đề chọn lọc sát với cấu trúc của bộ công bố. Khoá này bổ trợ cho khoá PRO XPLUS, với nhu cầu cần luyện thêm đề hay và sát cấu trúc.

Quý thầy cô giáo, quý phụ huynh và các em học sinh có thể mua Combo gồm cả 4 khoá học cùng lúc hoặc nhấn vào từng khoá học để mua lẻ từng khoá phù hợp với năng lực và nhu cầu bản thân.