Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 9: Tích của một vecto với một số chi tiết sách Toán 10 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 9: Tích của một vecto với một số
Giải Toán 10 trang 55 Tập 1 Kết nối tri thức
1. Tích của một vectơ với một số
HĐ1 trang 55 Toán lớp 10: Cho vecto AB→=a→. Hãy xác định điểm C sao cho BC→=a→
a) Tìm mối quan hệ giữa AB→ và a→+a→
b) Vecto a→+a→ có mối quan hệ như thế nào về hướng và độ dài đối với vecto a→
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải:
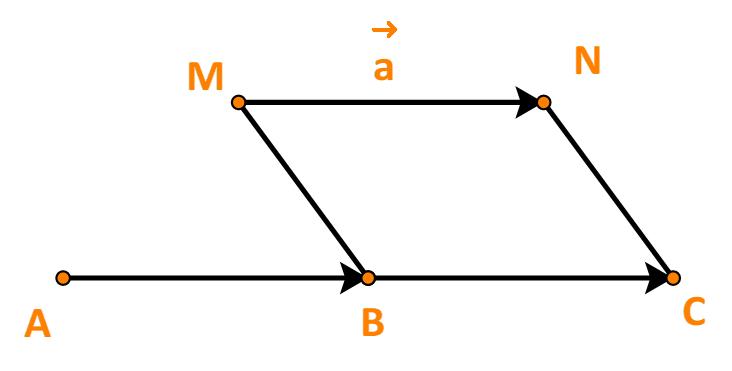
Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto a→.
Từ B, M, N ta dựng hình bình hành BMNC.
Khi đó: MN→=BC→ hay a→=BC→.
⇒a→+a→=AB→+BC→=AC→
a) Vì AB→=a→=BC→ nên A, B, C thẳng hàng và B là trung điểm của AC.
Vậy a→+a→ và AB→ cùng hướng, |a→+a→|=2.|AB→|
b) Ta có: a→+a→ và AB→ cùng hướng, |a→+a→|=2.|AB→|
Mà AB→=a→ nên: a→+a→ và a→ cùng hướng, |a→+a→|=2.|a→|.
Câu hỏi trang 55 Toán lớp 10: 1a→ và a→ có bằng nhau hay không?
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải:
Ta có: Vecto 1a→ cùng hướng với vecto a→ và |1a→|=|a→|.
Vậy hai vecto 1a→ và a→ bằng nhau.
Giải Toán 10 trang 56 Tập 1 Kết nối tri thức
HĐ2 trang 56 Toán lớp 10: Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số 0;1;2;−2. Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto OM→,ON→ với vecto a→=OA→. Viết đẳng thức thể hiện mối quan hệ giữa hai vecto OM→ và OA→.
Phương pháp giải:
Vecto ka→ (với k>0,a→≠0→) là vecto cùng hướng với vecto a→ và có độ đài bằng k|a→|.
Lời giải:
Dễ thấy:
Vecto OM→ và OA→có cùng giá nên chúng cùng phương.
Mà vecto OM→ và OA→cùng nằm trên tia OM nên chúng cùng chiều
Vậy vecto OM→ và OA→cùng hướng.
Ngoài ra, |OM→|=OM=2 và |OA→|=OA=1
⇒|OM→|=2.|OA→|
Ta kết luận OM→=2.OA→.
Câu hỏi trang 56 Toán lớp 10: −a→ và −1a→ có mối quan hệ gì?
Phương pháp giải:
Vecto ka→ (với k<0,a→≠0→) là vecto ngược hướng với vecto a→ và có độ đài bằng |k||a→|.
Lời giải:
Ta có:
Vecto −a→ là vecto đối của vecto a→
⇒−a→ ngược hướng với vecto a→ và |−a→|=|a→|
Lại có:
Vecto −1a→ là vecto ngược hướng với vecto a→ và có độ đài bằng |−1||a→|=|a→|.
⇒−a→ và −1a→ cùng hướng và có độ dài bằng nhau (bằng vectoa→).
Hay −a→=−1a→
Luyện tập 1 trang 56 Toán lớp 10: Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để AM→=t.AB→
b) Với điểm M bất kì, ta luôn có AM→=AMAB.AB→
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t≤0 để AM→=t.AB→
Phương pháp giải:
a→ và b→(b→≠0→) cùng phương khi và chỉ khi tồn tại số k để a→=k.b→
Nếu a→ và b→ cùng hướng thì k=|a→||b→|
Nếu a→ và b→ ngược hướng thì k=−|a→||b→|
Lời giải:
a) Điểm M thuộc đường thẳng d khi và chỉ khi hai vecto AM→ và AB→ cùng phương (cùng giá d)
Khi và chỉ khi tồn tại số t để AM→=t.AB→.
Vậy khẳng định a) đúng.
b) Với điểm M bất kì, ta luôn có AM→=AMAB.AB→
Sai vì AM→=AMAB.AB→ khi và chỉ khi AM→ và AB→ cùng hướng.
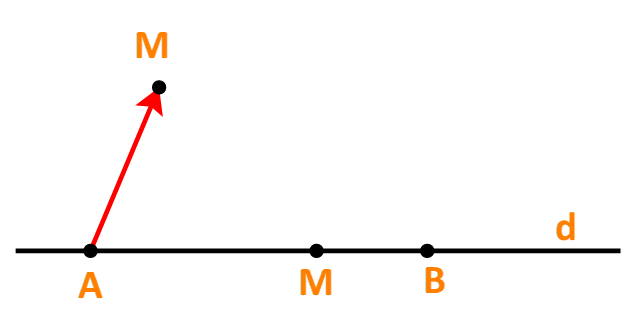
c) Điểm M thuộc tia đối của tia AB, tức là A nằm giữa M và B.
Khi và chỉ khi hai vecto AM→ và AB→ ngược hướng
⇔ tồn tại số t≤0 để AM→=t.AB→
Vậy khẳng định c) đúng.
2. Các tính chất của phép nhân vectơ với một số
Giải Toán 10 trang 57 Tập 1 Kết nối tri thức
HĐ3 trang 57 Toán lớp 10: Với u→≠0→ và hai số thực k, t, những khẳng định nào sau đây là đúng?
a) Hai vecto k(tu→) và (kt)u→ có cùng độ dài bằng |kt|.|u→|
b) Nếu kt≥0 thì cả hai vecto k(tu→), (kt)u→ cùng hướng với u→
c) Nếu kt<0 thì cả hai vecto k(tu→), (kt)u→ ngược hướng với u→
d) Hai vecto k(tu→) và (kt)u→ bằng nhau.
Phương pháp giải:
Vecto ka→ (với k>0,a→≠0→) cùng hướng với vecto a→ và có độ đài bằng k|a→|.
Vecto ka→ (với k<0,a→≠0→) ngược hướng với vecto a→ và có độ đài bằng |k||a→|.
Lời giải:
a) Hai vecto k(tu→) và (kt)u→ có cùng độ dài bằng |kt|.|u→|
Ta có: |tu→|=|t||u→|⇒|k(tu→)|=|k||(tu→)|=|k|.|t||u→|=|kt||u→|
Và |(kt)u→|=|kt||u→|
⇒|k(tu→)|=|(kt)u→|=|kt||u→|
b) Nếu kt≥0 thì cả hai vecto k(tu→), (kt)u→ cùng hướng với u→
Ta xét 2 trường hợp:
Trường hợp 1: k≥0,t≥0
Vecto k(tu→) cùng hướng với vecto tu→ (vì k≥0 ), mà vecto tu→ cùng hướng với vecto u→ (vì t≥0 )
Do đó vecto k(tu→) cùng hướng với vecto u→.
Trường hợp 2: k<0,t<0
Vecto k(tu→) ngược hướng với vecto tu→ (vì k<0 ), mà vecto tu→ ngược hướng với vecto u→ (vì t<0 )
Do đó vecto k(tu→) cùng hướng với vecto u→.
Vậy vecto k(tu→) luôn cùng hướng với vecto u→ nếu kt≥0.
Lại có: kt≥0 nên (kt)u→ cùng hướng với u→
Vậy kt≥0 thì cả hai vecto k(tu→), (kt)u→ cùng hướng với u→
c) Nếu kt<0 thì cả hai vecto k(tu→), (kt)u→ ngược hướng với u→
Ta xét 2 trường hợp:
Trường hợp 1: k>0,t<0
Vecto k(tu→) cùng hướng với vecto tu→ (vì k>0 ), mà vecto tu→ ngược hướng với vecto u→ (vì t<0)
Do đó vecto k(tu→) ngược hướng với vecto u→.
Trường hợp 2: k<0,t>0
Vecto k(tu→) ngược hướng với vecto tu→ (vì k<0 ), mà vecto tu→ cùng hướng với vecto u→ (vì t>0)
Do đó vecto k(tu→) ngược hướng với vecto u→.
Vậy vecto k(tu→) luôn ngược hướng với vecto u→ nếu kt<0.
Lại có: kt<0 nên (kt)u→ ngược hướng với u→
Vậy kt<0 thì cả hai vecto k(tu→), (kt)u→ ngược hướng với u→
d)
Từ ý b) và c), ra suy ra hai vecto k(tu→) và (kt)u→luôn cùng hướng.
Theo câu a) ta có: |k(tu→)|=|(kt)u→|=|kt||u→|
⇒ Hai vecto k(tu→) và (kt)u→ bằng nhau
HĐ4 trang 57 Toán lớp 10: Hãy chỉ ra trên Hình 4.26 hai vecto 3(u→+v→) và 3u→+3v→. Từ đó, nêu mối quan hệ giữa 3(u→+v→) và 3u→+3v→
Luyện tập 2 trang 57 Toán lớp 10: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có
OB→+OA→+OC→=3OG→.
Phương pháp giải:
G là trọng tâm của tam giác ABC thì GB→+GA→+GC→=0→
Với 3 điểm A, B, C bất kì, ta luôn có AB→+BC→=AC→
Lời giải:
Ta có: OA→=OG→+GA→; OB→=OG→+GB→; OC→=OG→+GC→
⇒OB→+OA→+OC→=OG→+GA→+OG→+GB→+OG→+GC→⇔OB→+OA→+OC→=3OG→+(GA→+GB→+GC→)
Do G là trọng tâm của tam giác ABC nên GB→+GA→+GC→=0→
⇒OB→+OA→+OC→=3OG→+0→⇔OB→+OA→+OC→=3OG→
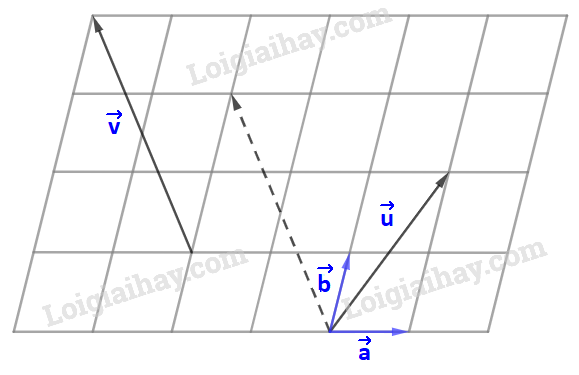
Luyện tập 3 trang 57 Toán lớp 10: Trong hình 4.27, hãy biểu thị mỗi vecto u→,v→ theo hai vecto a→,b→, tức là tìm các số x,y,z,t để u→=xa→+yb→,v→=ta→+zb→.
Phương pháp giải:
Phân tích vecto u→,v→ theo hai vecto a→,b→ cho trước.
Lời giải:
Bước 1: Dựng hình bình hành có cạnh song song với giá của vecto a→,b→ và đường chéo là vecto u→,v→.
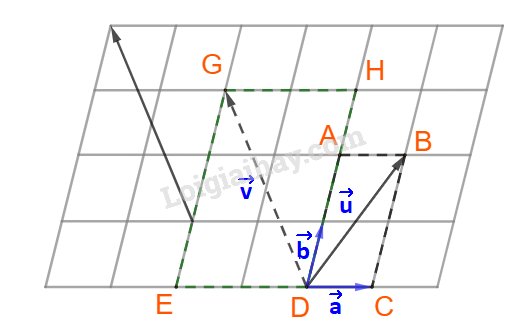
Ta dựng được hình hình hành ABCD và DEGH. Trong đó: DC và DE nằm trên giá của vecto a→, DA và DH nằm trên giá của vecto b→, còn vecto u→,v→ lần lượt là hai dường chéo.
Dễ thấy: u→=DA→+DC→,v→=DH→+DE→
Mà DA→=3b→,DC→=a→,DH→=3b→,DE→=−2a→.
⇒u→=2b→+a→,v→=3b→−2a→
Bài tập
Giải Toán 10 trang 58 Tập 1 Kết nối tri thức
Bài 4.11 trang 58 Toán lớp 10: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị AM→ theo hai vecto AB→ và AD→.
Bài 4.12 trang 58 Toán lớp 10: Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh BC→+AD→=2MN→=AC→+BD→.
Lời giải:
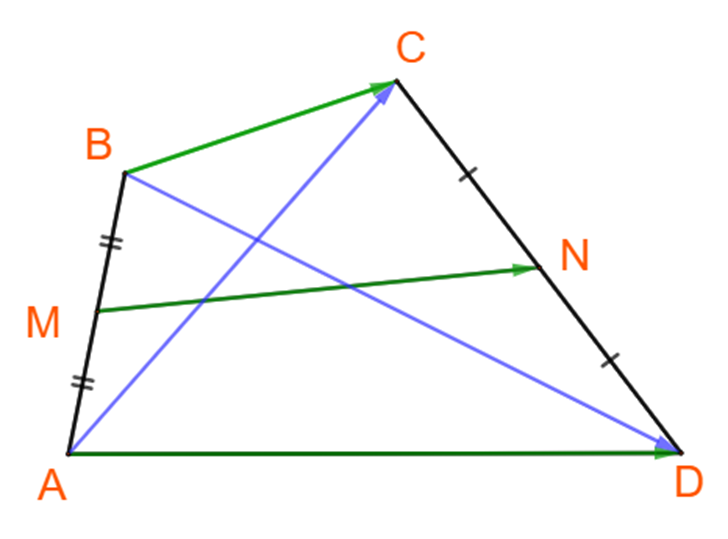
Ta có:
MN→=MA→+AD→+DN→
Mặt khác: MN→=MB→+BC→+CN→
⇒2MN→=MA→+AD→+DN→+MB→+BC→+CN→⇔2MN→=(MA→+MB→)+(DN→+CN→)+BC→+AD→⇔2MN→=0→+0→+BC→+AD→⇔2MN→=BC→+AD→
Tương tự ta cũng có:
{MN→=MA→+AC→+CN→MN→=MB→+BD→+DN→
⇒2MN→=MA→+AC→+CN→+MB→+BD→+DN→⇔2MN→=(MA→+MB→)+(CN→+DN→)+AC→+BD→⇔2MN→=0→+0→+AC→+BD→⇔2MN→=AC→+BD→
Vậy BC→+AD→=2MN→=AC→+BD→.
Bài 4.13 trang 58 Toán lớp 10: Cho hai điểm phân biệt A và B.
a) Hãy xác định điểm K sao cho KA→+2KB→=0→.
b) Chứng minh rằng với mọi điểm O, ta có OK→=13OA→+23OB→.
Lời giải:
a)
Cách 1:
Ta có: KA→+2KB→=0→.
⇔KA→=−2KB→
Suy ra vecto KA→ và vectoKB→ cùng phương, ngược chiều và KA=2.KB
⇒K,A,Bthẳng hàng, K nằm giữa A và B thỏa mãn: KA=2.KB
Cách 2:
Ta có: KA→+2KB→=0→.
⇔(KB→+BA→)+2KB→=0→⇔3.KB→+BA→=0→⇔3.KB→=AB→⇔KB→=13AB→
Vậy K thuộc đoạn AB sao cho KB=13AB.
b)
Để OK→=13OA→+23OB→.
⇒OK→=13(OK→+KA→)+23(OK→+KB→)⇔OK→=(13OK→+23OK→)+(13KA→+23KB→)⇔OK→=OK→+13(KA→+2KB→)⇔OK→=OK→+13.0→⇔OK→=OK→.
Hiển nhiên đúng với mọi điểm O.
Vậy với mọi điểm O, ta có OK→=13OA→+23OB→.
Chú ý khi giải:
Với những biểu thức đơn giản (chỉ có 3 điểm) thì từ giải thiết ta có thể suy ra ngay phương, chiều, độ dài của chúng để xác định điểm M.
Với các biểu thức phức tạp hơn (có nhiều hơn 3 điểm) thì nên sử dụng phương pháp như trên: quy về một vecto chưa biết, được biểu diễn qua các vecto đã biết.
Bài 4.14 trang 58 Toán lớp 10: Cho tam giác ABC
Bài 4.15 trang 59 Toán lớp 10: Chất điểm A chịu tác động của ba lực F1→,F2→,F3→ như hình 4.30 và ở trạng thái cân bằng (tức là F1→+F2→+F3→=0→). Tính độ lớn của các lực F2→,F3→ biết F1→ có độ lớn là 20N.
Lời giải:
Bước 1: Đặt u→=F1→+F2→. Ta xác định các điểm như hình dưới.
Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto u→ chính là vecto AC→
Vì chất điểm A ở trang thái cân bằng nên F1→+F2→+F3→=0→ hay u→+F3→=0→
⇔u→ và F3→ là hai vecto đối nhau.
⇔A là trung điểm của EC.
Bước 2:
Ta có: |F1→|=AD=20,|F2→|=AB,|F3→|=AC.
Do A, C, E thẳng hàng nên CAB^=180o−EAB^=60o
⇒CAD^=90o−60o=30o⇒{AC=ADcos30o=4033;AB=DC=AC.sin30o=2033.
Vậy |F2→|=2033,|F3→|=4033.
Lý thuyết Tích của một vectơ với một số
1. Tích của một vectơ với một số
• Tích của một vectơ a→≠0→ với một số thực k > 0 là một vectơ, kí hiệu là k a→, cùng hướng với vectơ a→ và có độ dài bằng k a→.
Ví dụ: Cho hình vẽ sau:
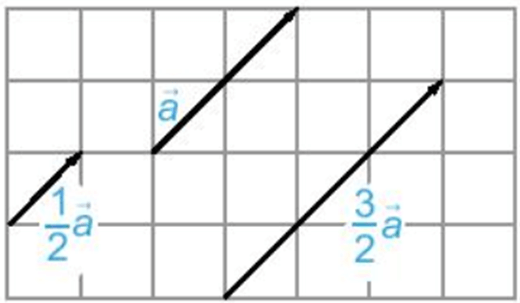
- Vectơ 12a→ cùng hướng với vectơ a→ và 12a→ = 12|a→|
- Vectơ 32a→ cùng hướng với vectơ a→ và 32a→= 32|a→|.
• Tích của một vectơ a→≠0→ với một số thực k < 0 là một vectơ, kí hiệu là k a→, ngược hướng với vectơ a→ và có độ dài bằng (-k) |a→|.
Ví dụ: Cho hình sau:
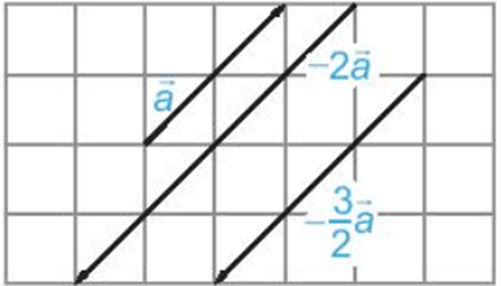
- Vectơ -2a→ ngược hướng với vectơ a→ và −2a→= 2|a→|
- Vectơ −32a→ ngược hướng với vectơ a→ và −32a→= 32|a→|.
Chú ý: Ta quy ước k a→ = 0→ nếu a→ = 0→ hoặc k = 0.
Nhận xét: Vectơ k a→ có độ dài bằng |k||a→| và cùng hướng với a→ nếu k ≥ 0, ngược hướng với a→ nếu a→ ≠ 0→ và k < 0.
Chú ý: Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với một số (hay phép nhân một số với vectơ).
2. Các tính chất của phép nhân vectơ với một số
Với hai vectơ a→, b→ và hai số thực k, t, ta luôn có :
+) k(ta→) = (kt) a→;
+) k (a→ + b→) = ka→ + kb→; k (a→ - b→) = ka→ - kb→;
+) (k + t) a→ = ka→ + ta→;
+) 1a→ = a→; (-1) a→ = -a→.
Nhận xét:
Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi IA→+IB→=0→.
Điểm G là trọng tâm của tam giác ABC khi và chỉ khi GA→+GB→+GC→=0→.
Ví dụ:
a) Cho đoạn thẳng CD có trung điểm I. Chứng minh với điểm O tùy ý, ta có OC→+OD→=2OI→.
b) Cho tam giác ABC có G là trọng tâm. Chứng minh rằng với điểm O tùy ý, ta có OA→+OB→+OC→+OD→=3OG→.
Hướng dẫn giải
a) Vì I là trung điểm của CD nên ta có IC→+ID→=0→.
Do đó OC→+OD→=(OI→+IC→)+(OI→+ID→) = 2OI→ + (IC→+ID→)= 2OI→ + 0→ = 2OI→.
Vậy, OC→+OD→=2OI→.
b) Vì G là trọng tâm tam giác ABC nên: GA→+GB→+GC→=0→.
Ta có OA→+OB→+OC→=(OG→+GA→)+(OG→+GB→)+(OG→+GC→)
= 3OG→+(GA→+GB→+GC→)=3OG→+0→=3OG→
Vậy OA→+OB→+OC→=3OG→.
Chú ý : Cho hai vectơ không cùng phương a→ và b→. Khi đó, mọi vectơ u→ đều biểu thị (phân tích) được một cách duy nhất theo hai vectơ a→ và b→, nghĩa là có duy nhất cặp số (x; y) sao cho u→ = xa→ + yb→.
Ví dụ : Cho tam giác ABC. Hãy xác định điểm M để MA→+3MB→+2MC→=0→.
Hướng dẫn giải
Để xác định vị trí của M, trước hết ta biểu thị AM→ (với gốc A đã biết) theo hai vectơ đã biết AB→,AC→.
MA→+3MB→+2MC→=0→
⇔ MA→+3(MA→+AB→)+2(MA→+AC→)=0→
⇔ 6MA→+3AB→+2AC→=0→
⇔ AM→=12AB→+13AC→
Lấy điểm E là trung điểm của AB và điểm F thuộc cạnh AC sao cho AF=13AC.
Khi đó AE→=12AB→ và AF→=13AC→. Vì vậy AM→=AE→+AF→.
Suy ra M là đỉnh thứ tư của hình bình hành EAFM.
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 8: Tổng và hiệu của hai vectơ
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vecto
Bài tập cuối chương 4